spiral bevel gear supplier

Changzhou Baoxin Gleason Spiral Bevel Gears Calculation

A spiral bevel gear is one with a spiral tooth flank as in Figure 1. The spiral is generally consistent with the curve of a cutter with the diameter dc. The spiral angle β is the angle between a generatrix element of the pitch cone and the tooth flank. The spiral angle just at the tooth flank center is called the mean spiral angle βm. In practice, the term spiral angle refers to the mean spiral angle.

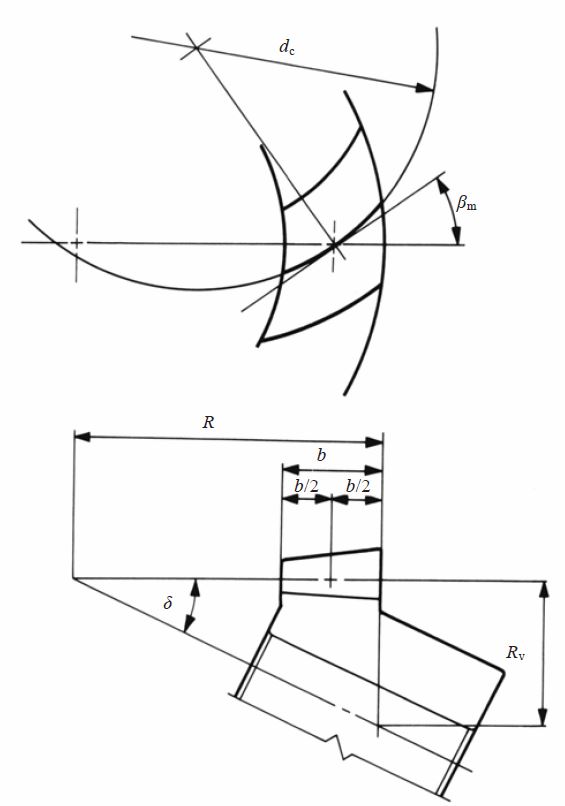
Fig.1 Spiral Bevel Gear (Left-hand)

All equations in Table 2 are specific to the manufacturing method of Spread Blade or of Single Side from Gleason. If a gear is not cut per the Gleason system, the equations will be different from these.

The tooth profile of a Gleason spiral bevel gear shown here has the tooth depth h = 1.888m; tip and root clearance c = 0.188m; and working depth hw = 1.700m. These Gleason spiral bevel gears belong to a stub gear system. This is applicable to gears with modules m > 2.1.

Table 1.8 shows the minimum number of teeth to avoid undercut in the Gleason system with shaft angle Σ = 90° and pressure angle αn = 20°.

Table 1.8 The minimum numbers of teeth to prevent undercut β=35°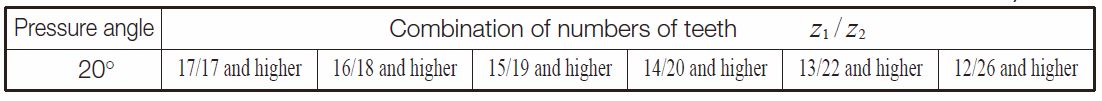

If the number of teeth is less than 12, Table 1.9 is used to determine the gear sizes.

Table 1.9 Dimentions for pinions with number of teeth less than 12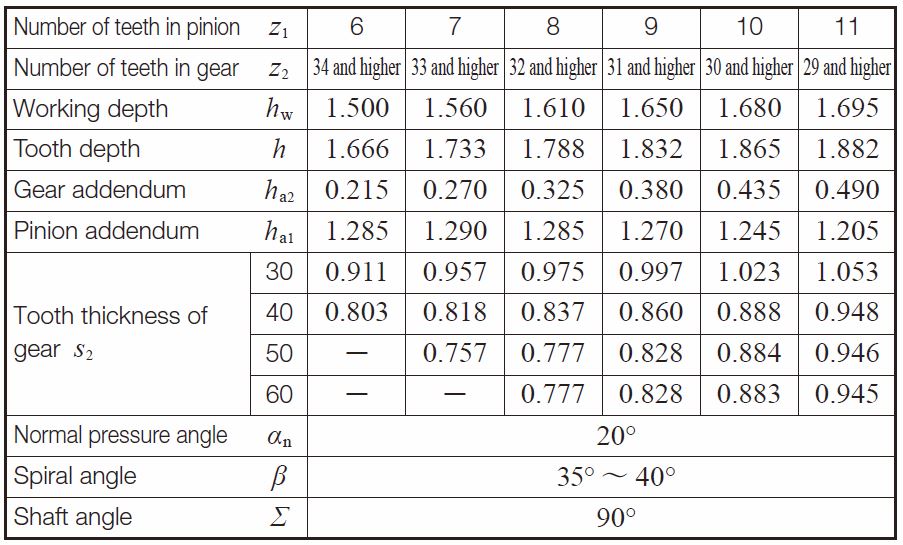

Table 2 shows the calculations for spiral bevel gears in the Gleason system

Table 2 The calculations for spiral bevel gears in the Gleason system

No.	Item	Symbol	Formula	Example
				Pinion (1)	Gesr (2)
1	Shaft angle	∑	Set Value	90 deg
2	Module	m		3
3	Normal pressure angle	αn		20 deg
4	Mean spiral angle	βm		35 deg
5	Number of teeth and spiral hand	z		20 (L)	40 (R)
6	Transverse pressure angle	αt		23.95680
7	Reference diameter	d	zm	60	120
8	Reference cone angle	σ1 σ2		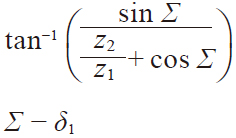26.56505 deg	63.43495 deg
9	Cone distance	R		67.08204
10	Facewidth	b	It should be less than 0.3R or 10m	20
11	Addendum	ha1 ha2		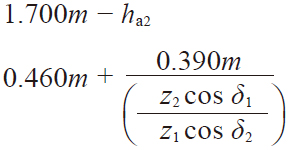3.4275	1.6725
12	Dedendum	hf	1.888m – ha	2.2365	3.9915
13	Dedendum angle	θf	tan^-1( hf / R )	1.90952 deg	3.40519 deg
14	Addendum angle	θa1 θa2	θf2 θf1	29.97024 deg	1.90952 deg
15	Tip angle	σa	σ + θa	29.97024 deg	65.34447 deg
16	Root angle	σf	σ – θf	24.65553 deg	60.02976 deg
17	Tip diameter	da	d + 2ha cos σ	66.1313	121.4959
18	Pitch apex to crown	X	R cos σ – ha sin σ	58.4672	28.5041
19	Axial facewidth	Xb		17.3565	8.3479
20	Inner tip diameter	di		46.1140	85.1224

All equations in Table 2 are also applicable to Gleason bevel gears with any shaft angle. A spiral bevel gear set requires matching of hands; left-hand and right-hand as a pair.

(4) Gleason Zerol Bevel Gears
When the spiral angle bm = 0, the bevel gear is called a Zerol bevel gear. The calculation equations of Table 4.16 for Gleason straight bevel gears are applicable. They also should take care again of the rule of hands; left and right of a pair must be matched. Figure 4.13 is a left-hand Zerol bevel gear.

Fig. 1.3 Left-hand zerol bevel gear

Baoxin's Manufacturing Capabilities

Leveraging German Gleason CNC gear milling machines to achieve high-precision physical realization of theoretical parameters:

Tooth Surface Processing

• Helical tooth flank profile tolerance ≤0.015mm (exceeds DIN 3965 Class AA)

• Crowning modification along tooth direction to compensate for elastic deformation (specialized for rolling mill gears)

Material and Heat Treatment

• Base material: 18CrNiMo7-6 carburizing steel (surface hardness HRC 60-62)

• Process: Controlled atmosphere nitriding with tooth root residual compressive stress ≥800MPa

Inspection System

• Full-parameter scanning via gear measuring center (Klingelnberg P65)

• Fatigue bench testing: 10^7 cycle loads (equivalent to 20 years of operational conditions)